强化学习简介

本篇为学习强化学习笔记，主要是学习李宏毅老师的课程的笔记。内容是强化学习的简单介绍，了解一下框架。

场景描述

强化学习的基本场景是Agent和Environment之间交互，Environment给出一个state，Agent看到了这个state（等同于observation，更好理解）并根据这个state做出某个Action，这个Action会影响Environment，state会发生改变，同时Environment会反馈一个Reward。

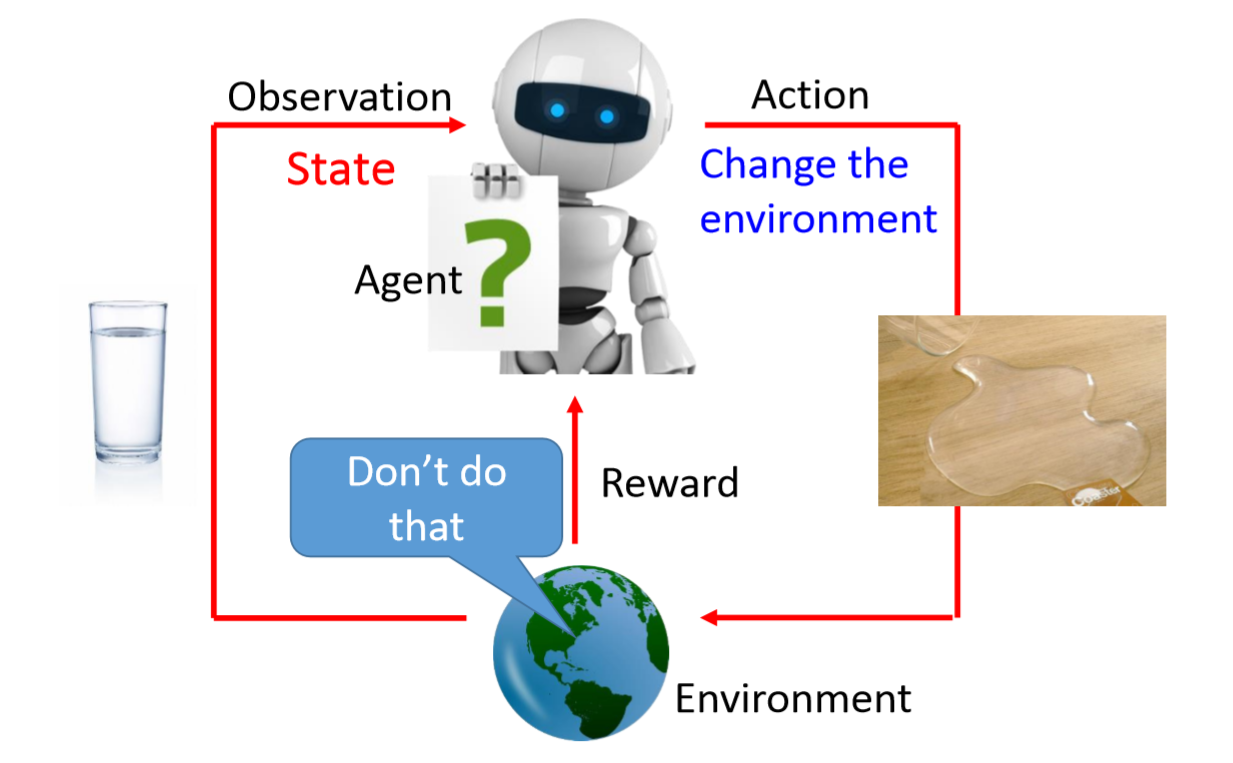
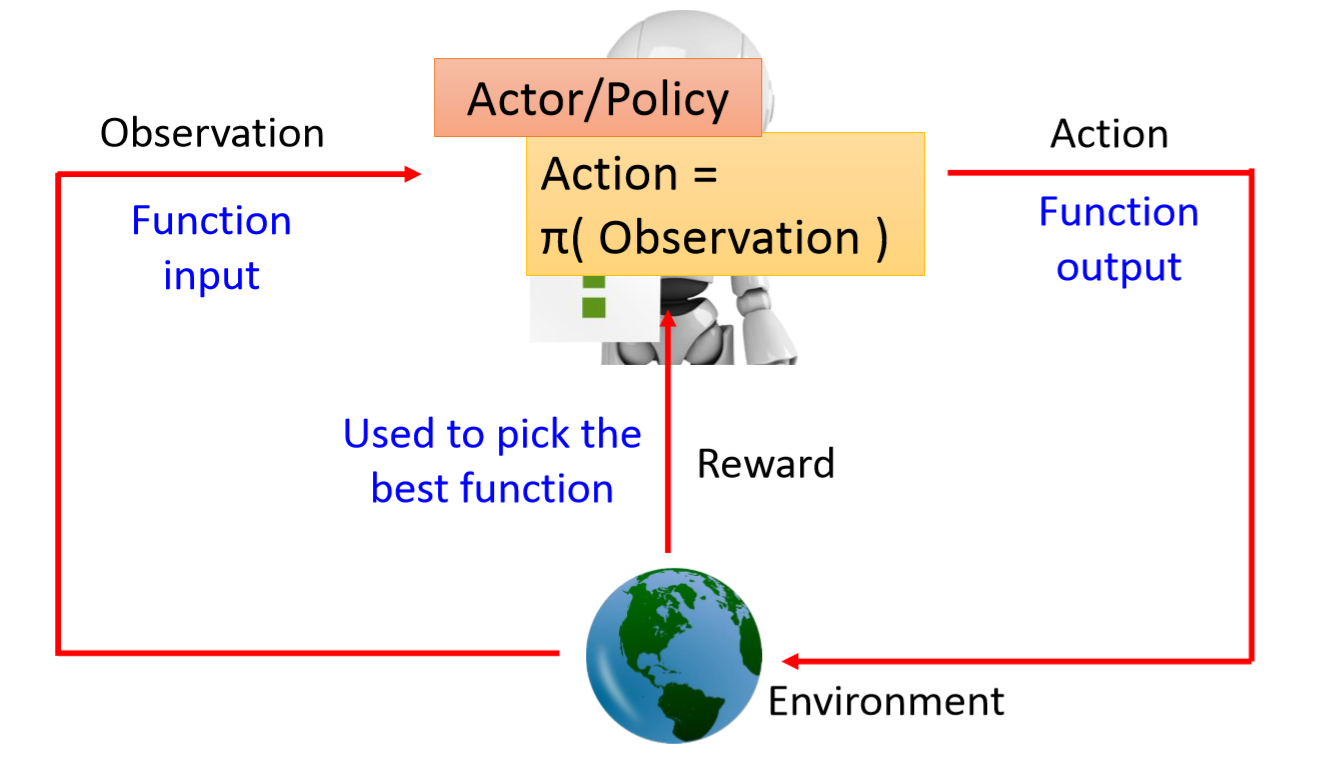
强化学习的目的，就是找到一个Actor或者叫Policy，让Reward最大，其输入使observation，输出是Action。

​

基本概念

以玩游戏为例。

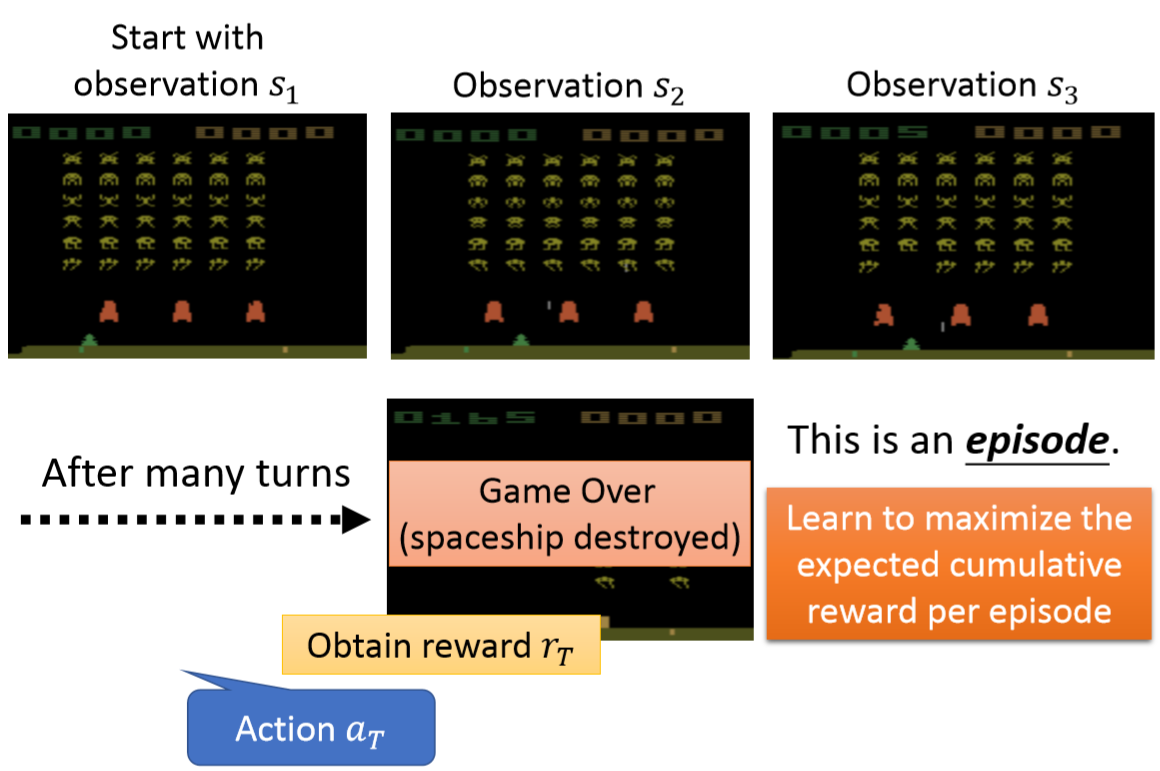
有以下概念：

• state: observation
• 玩一局游戏称为一个episode

​

分类

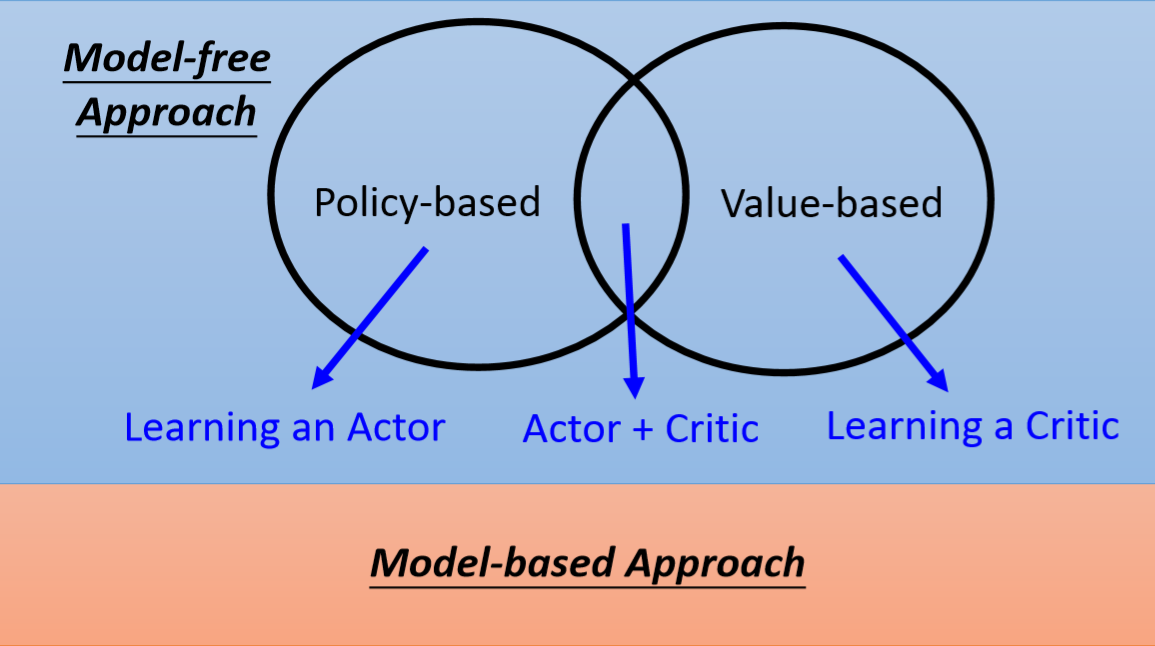
根据是否需要建模模拟环境，可以分为Model-free Approach（不需要对环境建模）和Model-based Approach，前者不需要对环境建模，后者需要。

Model-free Approach中，可以直接学习什么Actor(policy)最好，即Policy-based。也可以学习一个评估函数，来判断不同决策的价值是多少，即可得到每一步最好的Action。如果将两者结合起来则可以综合两方面的优势。

​

Policy-based Approach

问题介绍

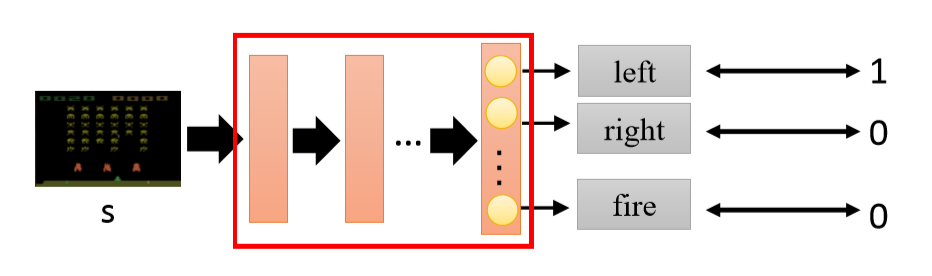
前面介绍了Policy-based Approach 就是要学习一个Actor，它会根据看到的情况来判断下一步动作，即输入是state（等同于observation），输出是Action。将神经网络的模型作为一个actor。以上面的游戏为例，其输入就是当前游戏画面，输出是需要进行的游戏操作，用$\pi_{\theta}(s)$来表示。

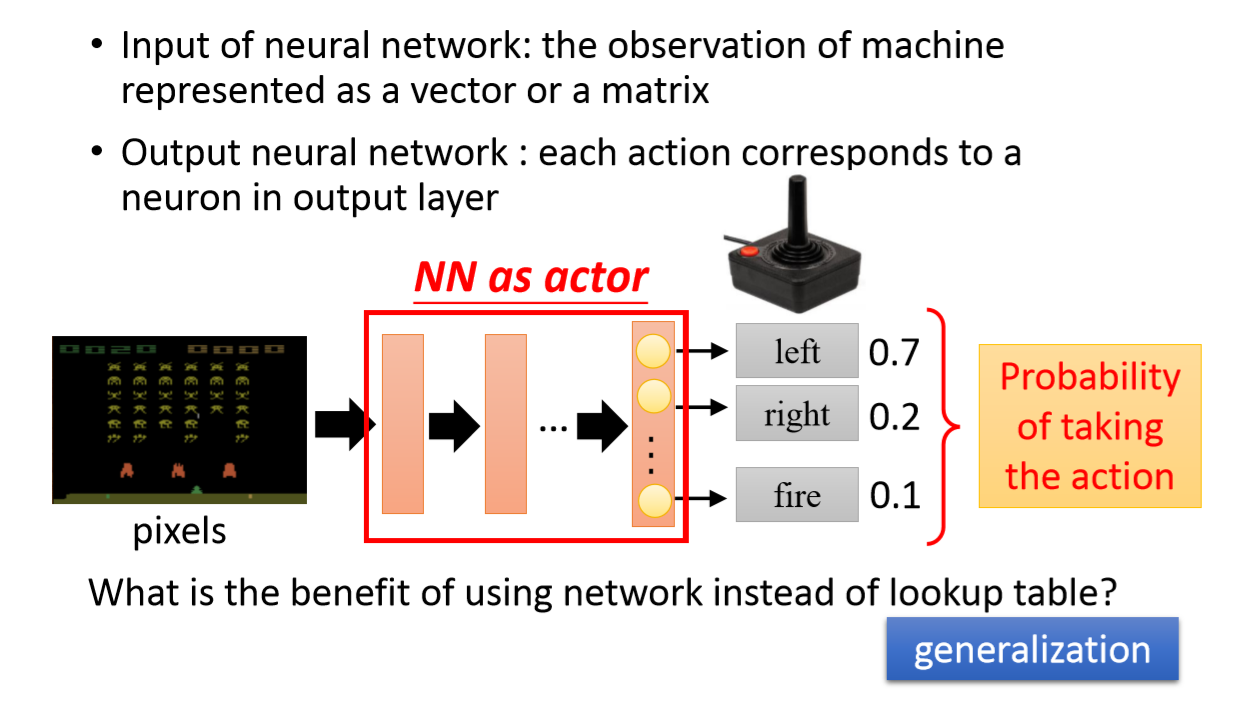
要训练这个神经网络模型，关键的问题是，它的训练目标是什么？强化学习的目标就是得到最多的奖励，所以应该用一个Actor所能得到的期望奖励作为评估其好坏的依据，可以通过蒙特卡洛法，多次实验用平均值作为期望值的矩估计。展开一个游戏过程来看，可以将游戏得分作为奖励，同一个Actor玩了很多局游戏，则用每局游戏奖励的平均值$\overline R_{\theta}$作为评估Actor $\pi_{\theta}(s)$好坏的依据。所以我们的只要将$\overline R_{\theta}$用$\theta$表示，最大化$\overline R_{\theta}$就可以。

​

Policy Gradient

将上面的问题抽象一下，就是找最优$\theta$，最大化$\overline R_{\theta}$。

梯度怎么求呢？这里$\overline R_{\theta}$是由episode的奖励$R(\tau)$和其概率$p(\tau|\theta)$决定，前者和Actor无关。这里对求导做了个变换，目的是为了把概率提出来，这样就可以表示成期望，然后利用蒙特卡洛来用均值代替。

注：这里通过乘$p(\tau|\theta)$后再除$p(\tau|\theta)$可以让该项可以表示成期望，但同时也将原来的$\nabla p(\tau|\theta)$变成了$\nabla log\ p(\tau|\theta)$，这会产生什么影响呢？$\nabla log\ p(\tau|\theta)$后面的求导中，还是会变成$1/p(\tau|\theta)$乘$\nabla p(\tau|\theta)$。原本更新$\theta$，按照$p(\tau|\theta)$的梯度反向传导，再用$R(\tau)$作为权重就可以了，前面这个$1/p(\tau|\theta)$是干啥的呢？是为了平衡样本偏差，本来应该完全按照$\tau$所带来的奖励决定其最终的概率，但现在样本是按照$p(\tau|\theta)$采样出来的，所以可能导致一个好的$\tau$在样本里极少出现，而未能对$\theta$的优化产生多大影响，所以$1/p(\tau|\theta)$就刚好是来解决这个问题。即：乘$p(\tau|\theta)$导致了偏差问题，再除$p(\tau|\theta)$有可以解决该问题。

$\nabla log\ p(\tau|\theta)$怎么求呢？将一局游戏(episode)拆开，可以表示为$\tau =\{s_1,a_1,r_1,s_2,a_2,r_2,···,s_T,a_T,r_T \}$，其似然为给定actor时产生该$\tau$的概率：$P(\tau|\theta)$。对其展开，整个游戏过程可以看做：给定了一个初始的状态$s_1$之后，Actor根据其观测到状态$s_t$和自身参数$\theta$产生一个动作$a_t$，环境根据状态$s_t$和Actore做出的动作$a_t$给出奖励$r_t$和下一各状态$s_{t+1}$。

$p(s_1)$表示初始状态是$s_1$的概率，由环境决定，不受Actor影响；$p(a_t|s_t,\theta)$表示其观测到状态$s_t$和自身参数$\theta$产生一个动作$a_t$的概率；$p(r_t,s_{t+1}|s_t,a_t)$表示Actor在$s_t$状态下做出动作$a_t$之后，得到的这局游戏中实际观测到的奖励$r_t$和下一个状态$s_{t+1}$的概率，这个概率也由环境决定，不受actor影响。所以似然中，只有$p(a_t|s_t,\theta)$与要优化的Actor相关。

将$p(\tau|\theta)$的计算公式代入$\nabla log\ p(\tau|\theta)$，其中只有$p(a_t|s_t,\theta)$与Actor相关。

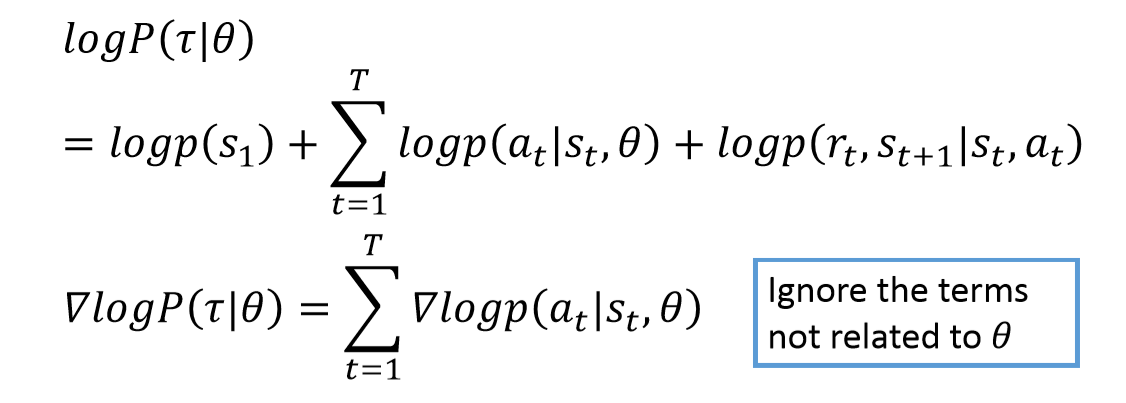
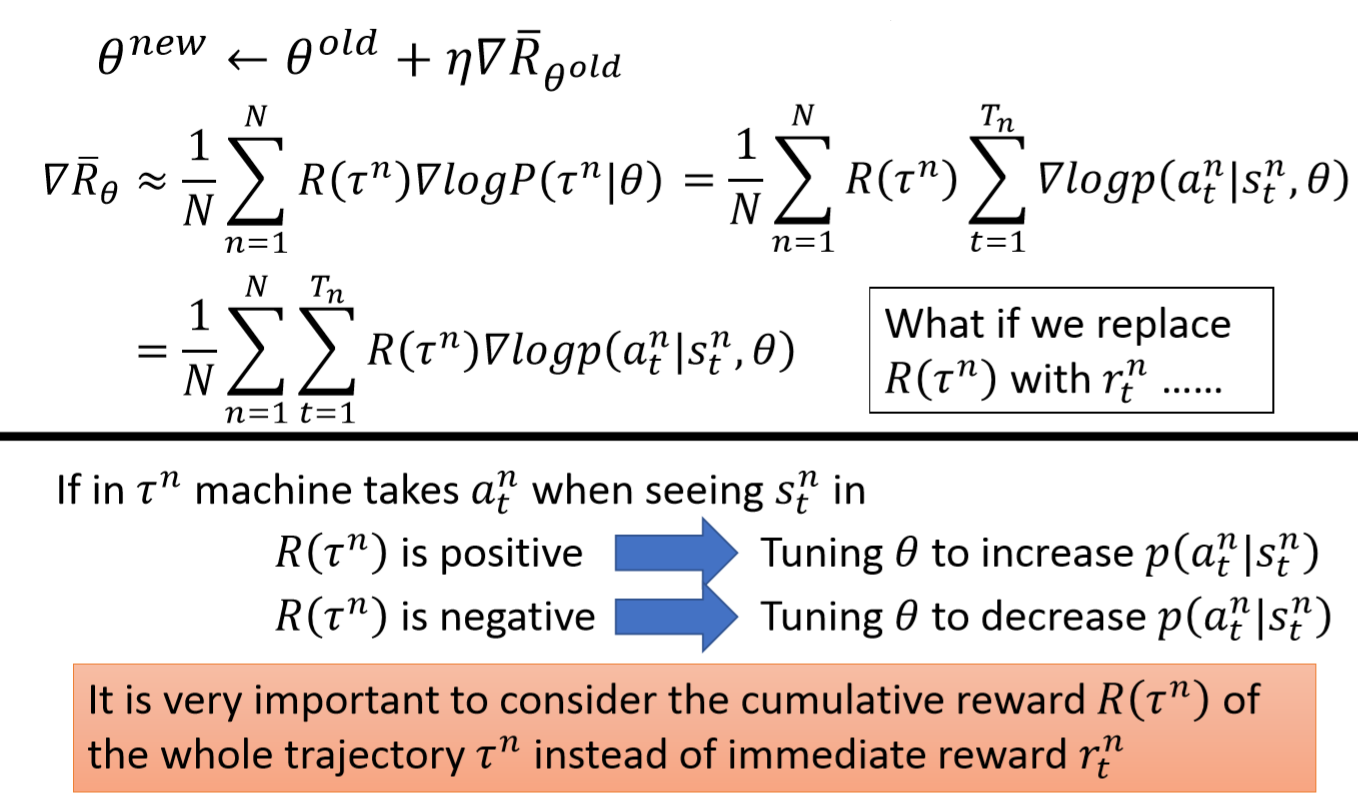
代入$\nabla\overline R_{\theta}$中，得到更新公式

​

总结一下

Actor的学习，就是要解决以下问题，我这里用期望代替均值，感觉表述更加准确。

$$\theta ^* = arg\ \underset{\theta}{max}\ E[R_{\theta}]$$

其中$E[R_{\theta}]$可以表示为

$$E[R_{\theta}] = \sum_{\tau} R(\tau) P(\tau|\theta)$$

其导数为

$$\begin{eqnarray*} \nabla E[R_{\theta}] &=& \nabla\sum_{\tau} R(\tau) P(\tau|\theta) \\ \\ &=& \sum_{\tau} R(\tau) \nabla P(\tau|\theta) \tag{$R(\tau)$与$\theta$无关} \\ \\ &=& \sum_{\tau} R(\tau)P(\tau|\theta) \frac{\nabla P(\tau|\theta)}{P(\tau|\theta)} \tag{增加$P(\tau|\theta)$凑为期望} \\ \\ &=& \sum_{\tau}P(\tau|\theta) R(\tau) \nabla log P(\tau|\theta) \tag{换为log导数} \\ \\ &\approx& \frac{1}{N}\sum^N_{n=1}R(\tau^n)\nabla log P(\tau^n|\theta) \tag{期望用均值代替} \end{eqnarray*}$$

其中$P(\tau|\theta)$可以展开其生成过程，并对其展开，并求解一下

$$\begin{eqnarray*} P(\tau|\theta) &=& p(s_1)\prod ^T_{t=1}p(a_t|s_t,\theta)p(r_t,s_{t+1}|s_t,a_t) \\ \\ log\ P(\tau|\theta) &=& log\ p(s_1) + \sum ^T_{t=1}\left [log\ p(a_t|s_t,\theta) + log \ p(r_t,s_{t+1}|s_t,a_t)\right ] \\ \\ \nabla log P(\tau|\theta) &=& \sum ^T_{t=1}\nabla log p(a_t|s_t,\theta) \end{eqnarray*}$$

因此

$$\begin{eqnarray*} \nabla E[R_{\theta}] &\approx& \frac{1}{N}\sum^N_{n=1}R(\tau^n)\nabla log P(\tau^n|\theta) \\ \\ &=& \frac{1}{N}\sum^N_{n=1}\sum ^{T_n}_{t=1}R(\tau^n)\nabla log p(a^n_t|s^n_t,\theta) \tag{仅$p(a_t|s_t,\theta)$与$\theta$相关} \\ \\ \end{eqnarray*}$$

​

视作多分类

这其实和多分类问题相同。如果将学习Actor看做一个多分类问题，数据就是在每局游戏中Actor实际根据状态做出的动作。

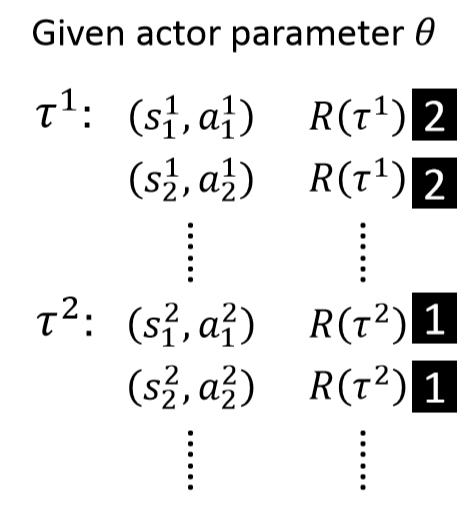
其中每个$(s,a)$对中，$s$作为输入，$a$作为输出，对应episode的$R(\tau)$作为权重。

多分类交叉熵为

$$J_{CE}(\theta) = -\frac1N \sum^{N}_{i=1}log(\hat y_{iy_i})$$

此处的$y_{i}$指的就是对应的$a$，$\hat y_{iy_i}$即$p(a^n_t|s^n_t,\theta)$，总样本数量为$N×T$个，权重为$R(\tau)$，则

$$J(\theta) =-\frac{1}{N×T}\sum^N_{n=1}\sum ^{T}_{t=1}R(\tau^n) log\ p(a^n_t|s^n_t,\theta)$$

这里全面的求平均是除$N×T$（实际上这样表示不准确，因为每个episode不一定都是T步），和上面Actor的公式有一点不一样，因为Actor是最大化的一次episode的联合概率，这里是拆解成动作，最大化每个动作的概率。

​

BaseLine

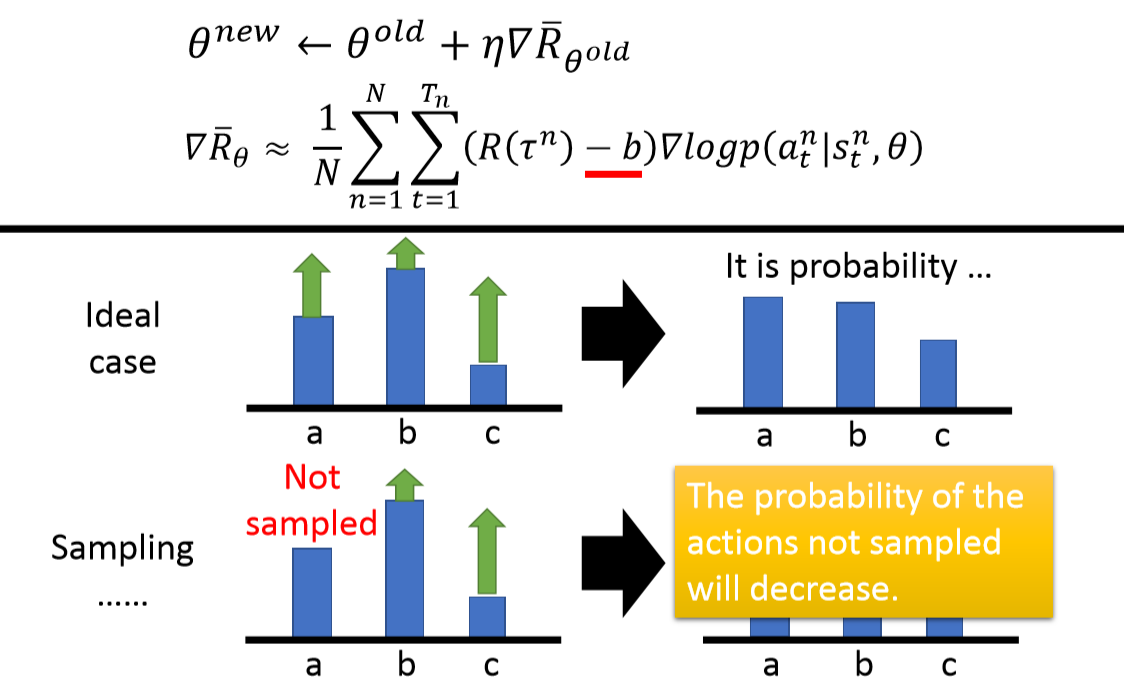
在这个案例中，奖励$R(\tau)$永远是正的，在数据量非常大的时候这样也没什么问题，因为Actor一次做出各种动作的概率和为1，即使较差的动作对应的权重$R(\tau)$也是正的，但应该没有较好的动作权重高，因此最终差的动作概率还是会下降。但实际训练中，数据是采样得到的，有可能真正好的动作没有采样到（下图的a），这样就会导致优秀的动作a的概率下降，差一点的b,c概率上升。解决这个问题，可以给奖励，加一个baseline，低于base line奖励为负。

​

Value-based Approach

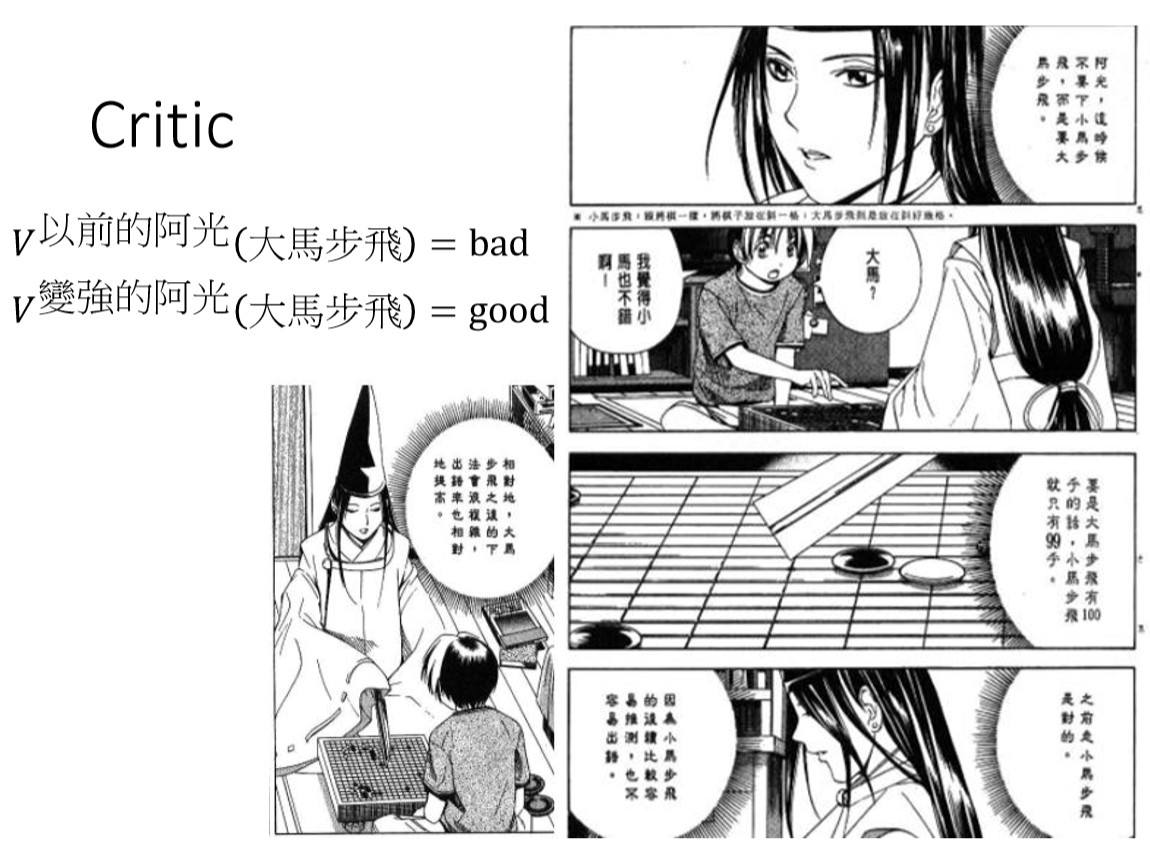
Value-based方法指学习一个Critic来判断Actor的好坏。Critic不决定Action，但可以从Critic得到一个最优的Actor。Critic分为两种：

1. $V^{\pi}(s)$ ：在看见状态$s$后，使用Actor $\pi$产生的累积奖励的期望值
2. $Q^{\pi}(s,a)$：在看见状态$s$后，先采取Action $a$，然后使用Actor $\pi$产生的累积奖励的期望值

比如说阿光在下棋的时候，旁边佐为会告诉他，现在的他能驾驭大马步飞了，下大马步飞是好棋，以前太弱不能这么下。

​

estimate $V^{\pi}(s)$

估计$V^{\pi}(s)$ 有两种方法：蒙特卡洛法和差分法

​

Monte-Carlo based approach

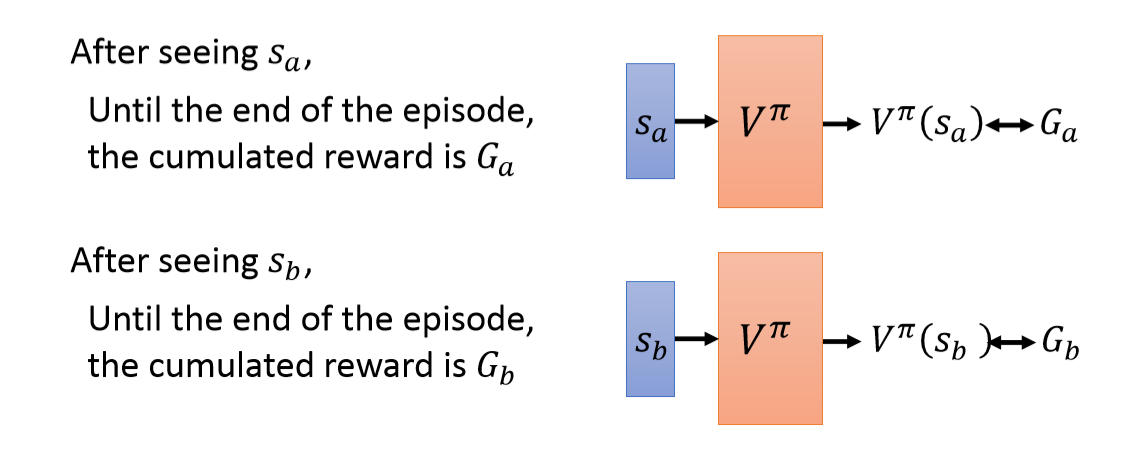
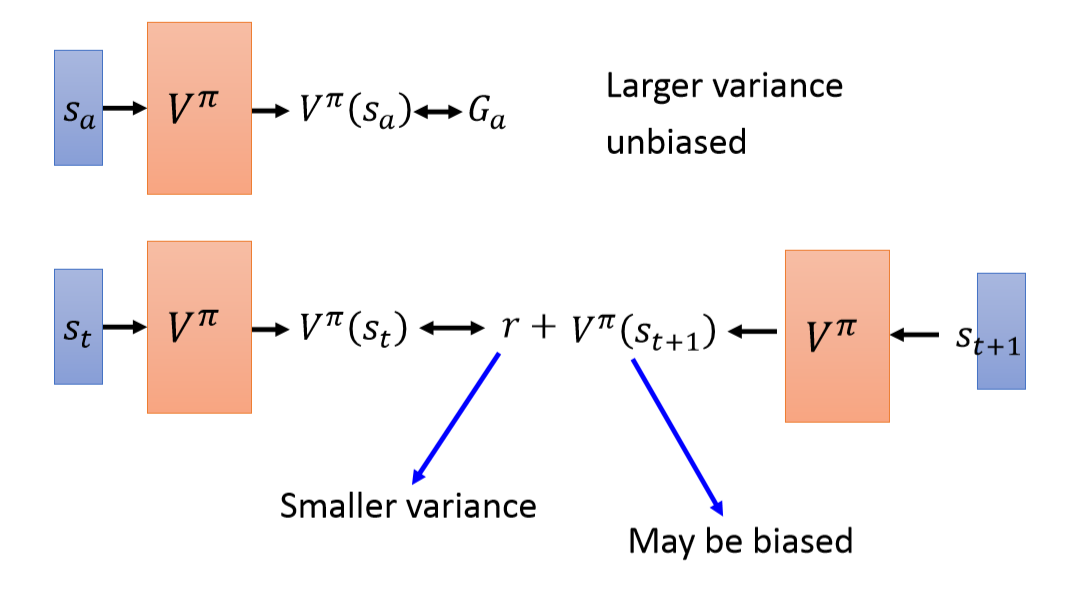
蒙特卡洛法就是让Actor $\pi$玩游戏，产生episode，来训练critic。在看见状态$s_a$之后，直到游戏结束产生的累积奖励为$G_a$。这里的$G$和之前每个episode的总奖赏$R$不同，$G$表示转态$s_a$之后的累计奖励。

​

Temporal-difference approach

差分法，策略$\pi$下产生的episode，相邻状态$s_t$和$s_{t+1}$下的$V$值相差$r_t$，可以以此为目标训练$V^{\pi}(s)$ 。

​

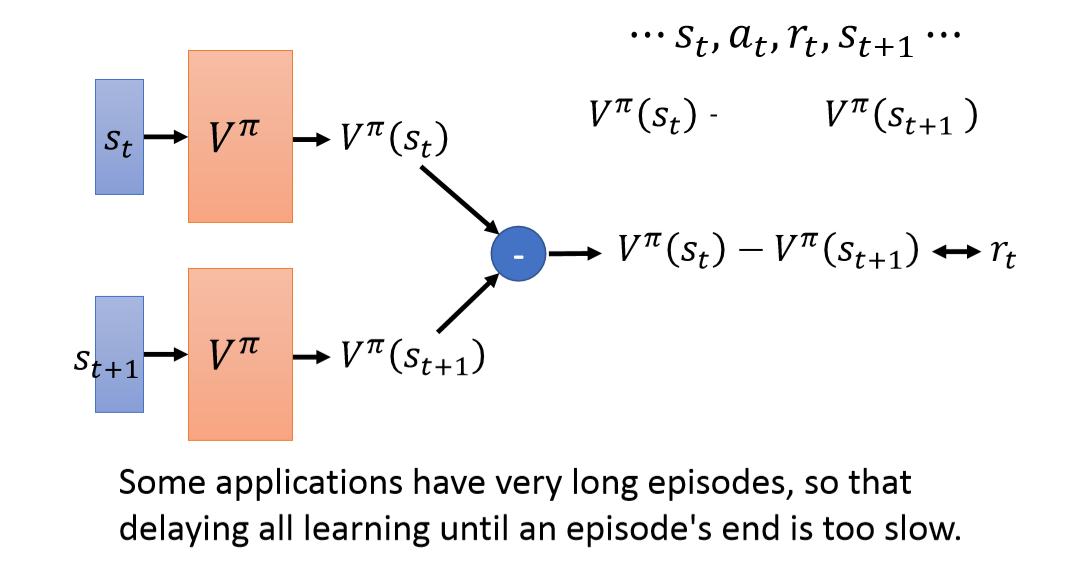
MC vs TD

第一点是目标值的方差和偏差的不同。MC法直接预测的是累积奖励$G_a$，方差会更大。而TD法，标签值是单步的$r$，方差相对小，但其用到了$V^{\pi}(s_{t+1})$，这个值一定准。

第二点是基于的假设不同。在下面的数据中，一共有8个episode，不管我们用哪个方法，很明显都能得到$V^{\pi}(s_{b})=3/4$，那么$V^{\pi}(s_{a})$应该等于多少呢。按照MC方法，$V^{\pi}(s_{a})=0$（只有一条数据）；按照TD方法，$V^{\pi}(s_{a})=V^{\pi}(s_{b})+0=3/4$。MC的假设下状态前后之间可能有相互影响。

​

问题：

1. 看起来针对不同的Actor $\pi$有一个模型$V^{\pi}(s)$， Actor如果更新了，V要重新训练吗？

2. 得到这个V之后如何使用？

3. MC和TD之间的假设差异如何理解？

​

Q-Learning

Q-Learning一样可以用MC和TD方法。学习的目标是$Q^{\pi}(s,a)$

​

Actor-Critic