常见的分布

总结常见的分布

离散型

二点分布

表示：$X\sim b(1,p)$

别名：0-1分布；伯努利分布

分布列：$P(X=x)=p^x(1-p)^{1-x},x=0,1.$

二项分布

表示：$X\sim b(n,p)$

分布列：

$$\begin{eqnarray*} P(X=k) &=& \binom{n}{k}p^k(1-p)^{n-k} \tag{$\binom{n}{k}$种可能的概率都是$p^k(1-p)^{n-k}$} \\ \\ &=& \frac{n!}{k!(n-k)!}p^k(1-p)^{n-k} \end{eqnarray*}$$

含义：n重伯努利实验中成功的次数

分布特征

$$\begin{eqnarray*} E(X) &=& \sum^n_{k=0} k\ \binom{n}{k}p^k(1-p)^{n-k} \\ \\ &=& np \sum^n_{k=1} \binom{n-1}{k-1}p^{k-1}(1-p)^{(n-1)-(k-1)} \tag{从$C^k_n$中提出n,约掉k} \\ \\ &=& np[p+(1-p)]^{n-1} \tag{二项定理} \\ \\ &=& np \\ \\ Var(X) &=& E(X^2)-(E(X))^2 \\ \\ &=& np(1-p) \tag{$E(X^2)$证明复杂，省略} \end{eqnarray*}$$

二项定理

$$\begin{eqnarray*} (x+y)^n &=& \sum^n_{k=0} \binom{n}{k} x^{n-k}y^k = \sum^n_{k=0} \binom{n}{k} x^{k}y^{n-k} \\ \\ \binom{n}{k} &=& C^k_n = \frac{n!}{k!(n-k)!} \end{eqnarray*}$$

分布图

• 位于均值np附近的概率较大
• 随着p的增加，分布的峰逐渐右移

泊松分布

连续型

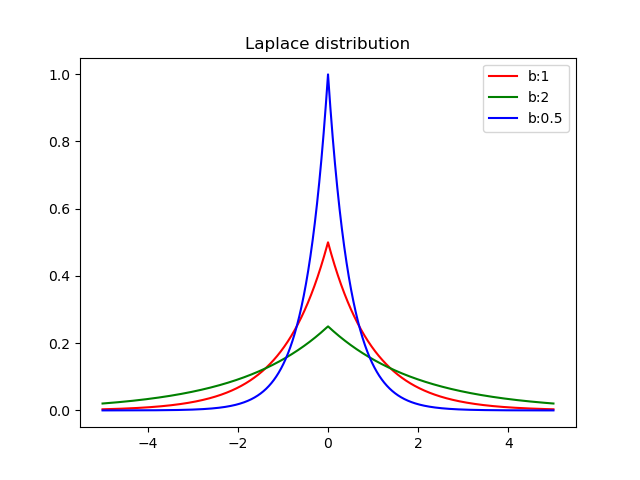
正态分布

表示：$X\sim N(\mu,\sigma^2)$

别名：高斯分布，Normal distribution

含义：（中心极限定理）一个随机变量如果是大量微小的，独立的随机因素的叠加结果，则可认为服从正态分布。

• 测量误差
• 产品重量
• 人的身高
• 年降雨量

分布表示

$$\begin{eqnarray*} p(x) &=& \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} ,\ -\infty<x<+\infty \\ \\ F(x) &=& \frac{1}{\sqrt{2\pi}\sigma} \int^x_{-\infty}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt ,\ -\infty<x<+\infty \end{eqnarray*}$$

分布特征

$$\begin{eqnarray*} E(X)&=&\mu \\ \\ Var(X)&=&\sigma^2 \end{eqnarray*}$$

分布图

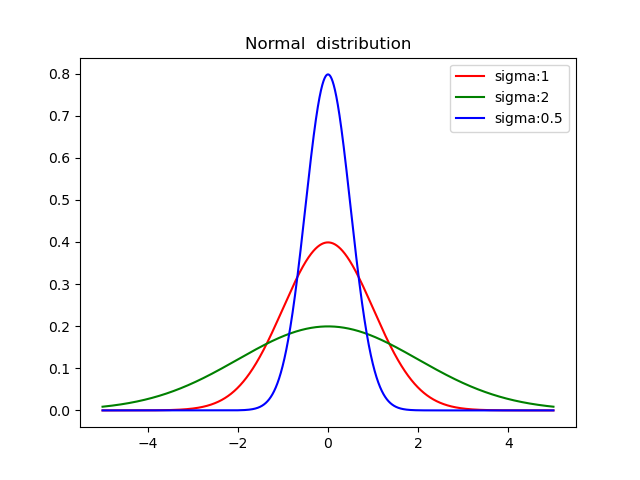
拉普拉斯分布

表示：$X\sim Laplace(\mu,b)$

别名：双指数分布，Laplace distribution

含义：由两个指数函数组成的

分布表示

$$\begin{eqnarray*} p(x) &=& \frac{1}{2b}e^{-\frac{|x-\mu|}{b}} \\ \\ F(x) &=& \frac12 \left[ 1+sgn(x-\mu)(1-e^{-\frac{|x-\mu|}{b}}) \right ] \end{eqnarray*}$$

分布特征

$$\begin{eqnarray*} E(X)&=&\mu \\ \\ Var(X)&=&2b^2 \end{eqnarray*}$$

分布图