激活函数

在深度学习中，激活函数提供了非线性变换的能力，提高了神经网络的表达能力。根据万能近似定理，这种非线性表达能力赋予了神经网络拟合一切函数的能力！当然也让大多数我们感兴趣的代价函数都变得非凸。

激活函数基本性质

关于激活函数的一些问题

1. 激活函数的作用

   激活函数是用来加入非线性因素的，提高神经网络对模型的表达能力，解决线性模型所不能解决的问题

2. 激活函数一般需要具有的几个性质

   • 有界
   • 容易求导
   • 单调(容易进行凸优化)
   • 处理简单(计算方面)

参考

机器之心：26种神经网络激活函数可视化

Activation Functions: Comparison of trends in Practice and Research for Deep Learning

常见的激活函数

sigmoid

函数形式

$$\begin{eqnarray*} sigmoid(z) &=& \frac{ 1 }{ 1+e^{−z} } \\ \\ sigmoid′(z) &=& \frac { e^{-z} } { (1+e^{-z})^2 } = sigmoid(z)(1-sigmoid(z)) \tag{一阶导数} \end{eqnarray*}$$

经常用$\sigma (·)$表示。

函数形状

sigmoid函数形状

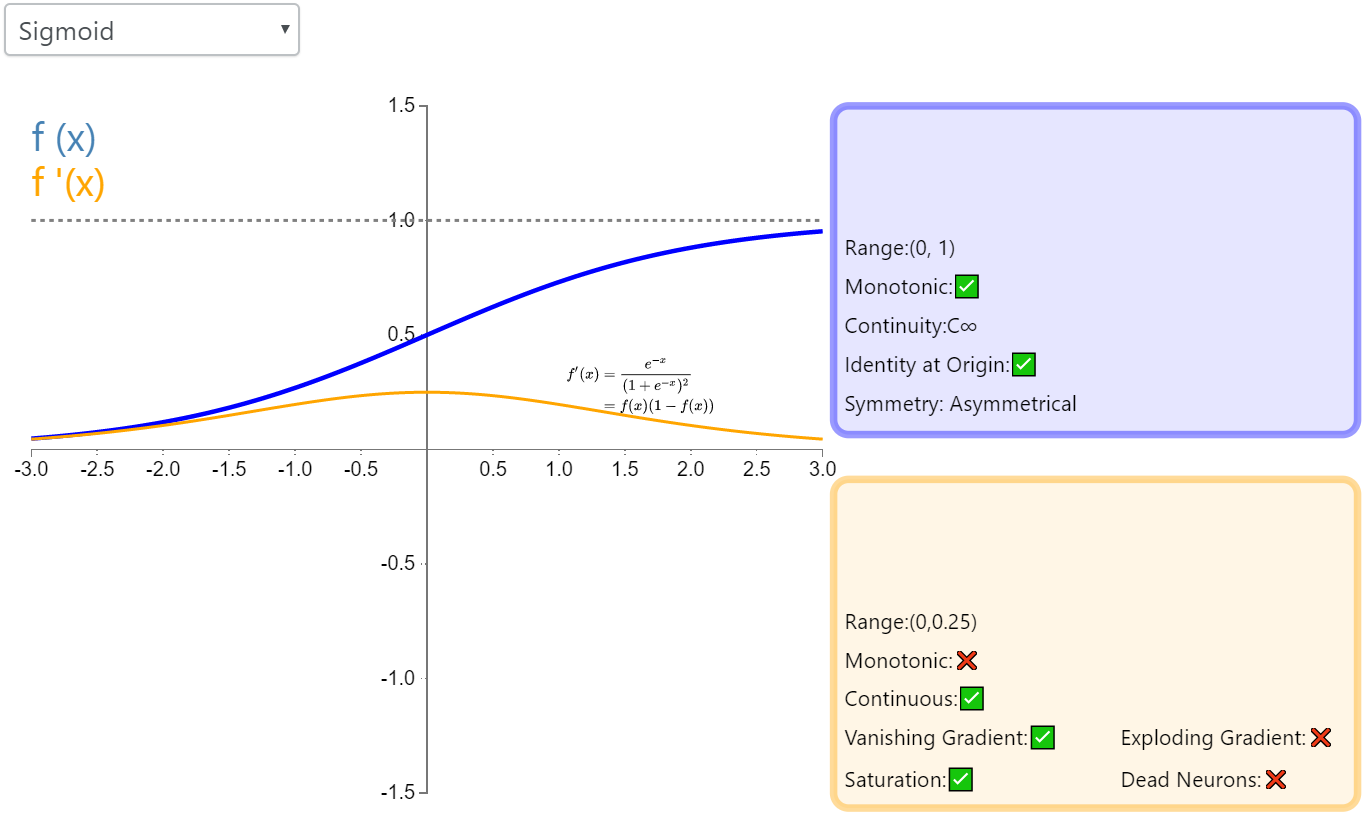
作为激活的特点

输出是0~1之间

因此，在LSTM的三个门中使用的激活函数就是sigmoid。

作为激活函数的缺点

1. 因为sigmoid函数的梯度最大值是0.25，容易梯度消失
2. 不是0均值，0均值有什么作用

关于sigmoid函数的起源

tanh函数

函数形式

$$\begin{eqnarray*} tanh(x)&=&\frac{e^x-e^{-x}}{e^x+e^{-x}} \\ \\ tanh^{\prime}(x)&=&\frac{(e^x+e^{-x})(e^x+e^{-x})-(e^x-e^{-x})(e^x-e^{-x})}{(e^x+e^{-x})^2} \\ \\ &=& 1- \frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \\ \\ &=& 1- tanh^2(x) \end{eqnarray*}$$

函数形状

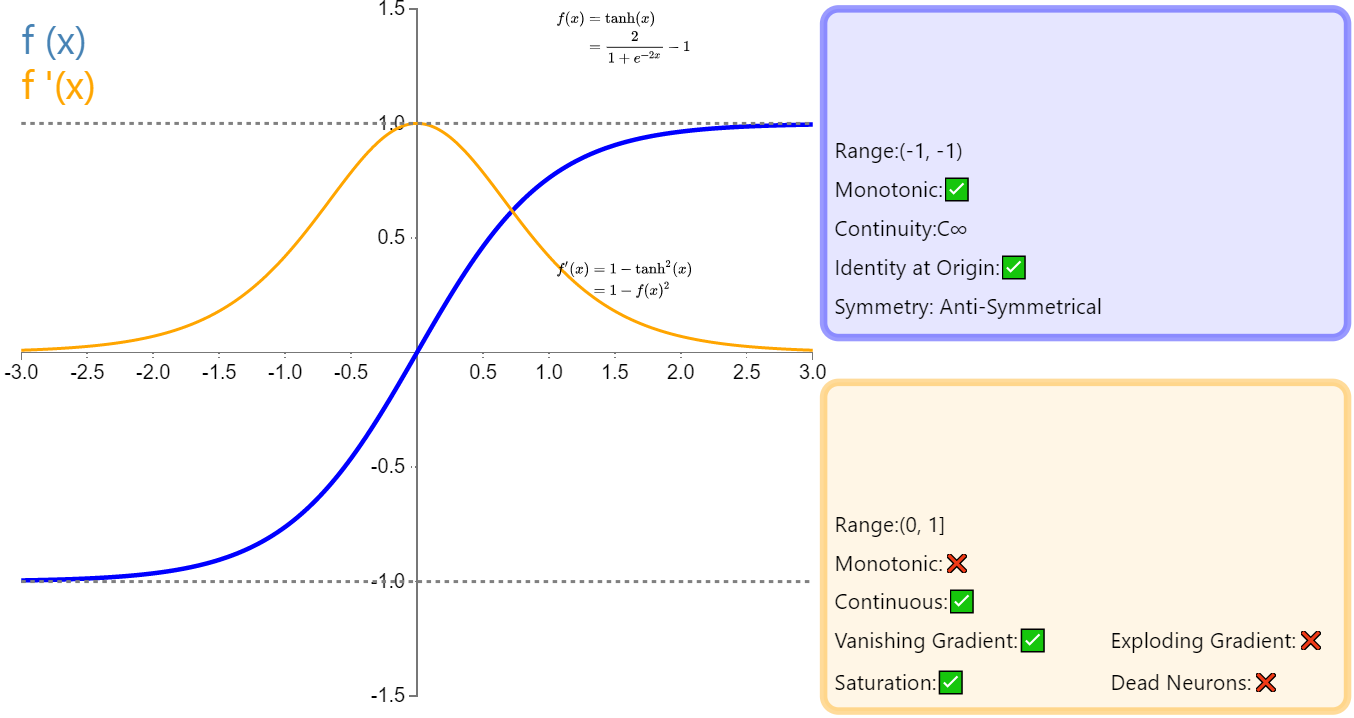
函数的特点

• 优点：0均值
• 缺点：梯度消失
• 曾应用广泛

Relu函数

函数形式

$$Relu(x) = max(0,x)$$

函数形状

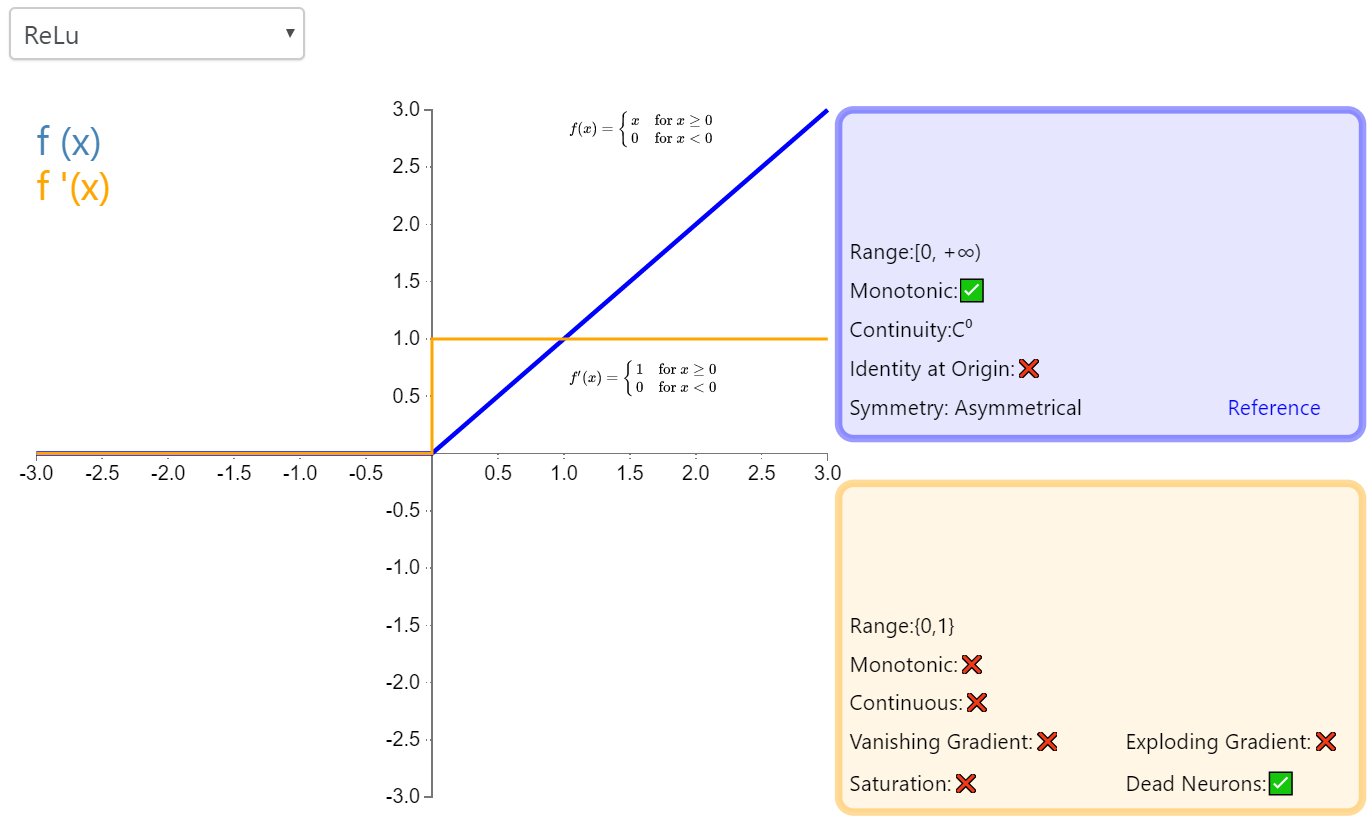
修正线性单元（Rectified linear unit，ReLU）

特点

• 优点：计算速度快，稀疏，梯度消失缓解
• 缺点：神经元会死亡
• 应用广泛

Leaky Relu

带泄露修正线性单元（Leaky ReLU）

函数形式

$$\begin{eqnarray*} f(x)&=&\left\{\begin{array}{ll} x&\text{for $x \geq 0$}\\ 0.01x &\text{for $x<0$}. \end{array}\right. \\ \\ f^{\prime}(x)&=&\left\{\begin{array}{ll} 1&\text{for $x \geq 0$}\\ 0.01 &\text{for $x<0$}. \end{array}\right. \end{eqnarray*}$$

函数形状

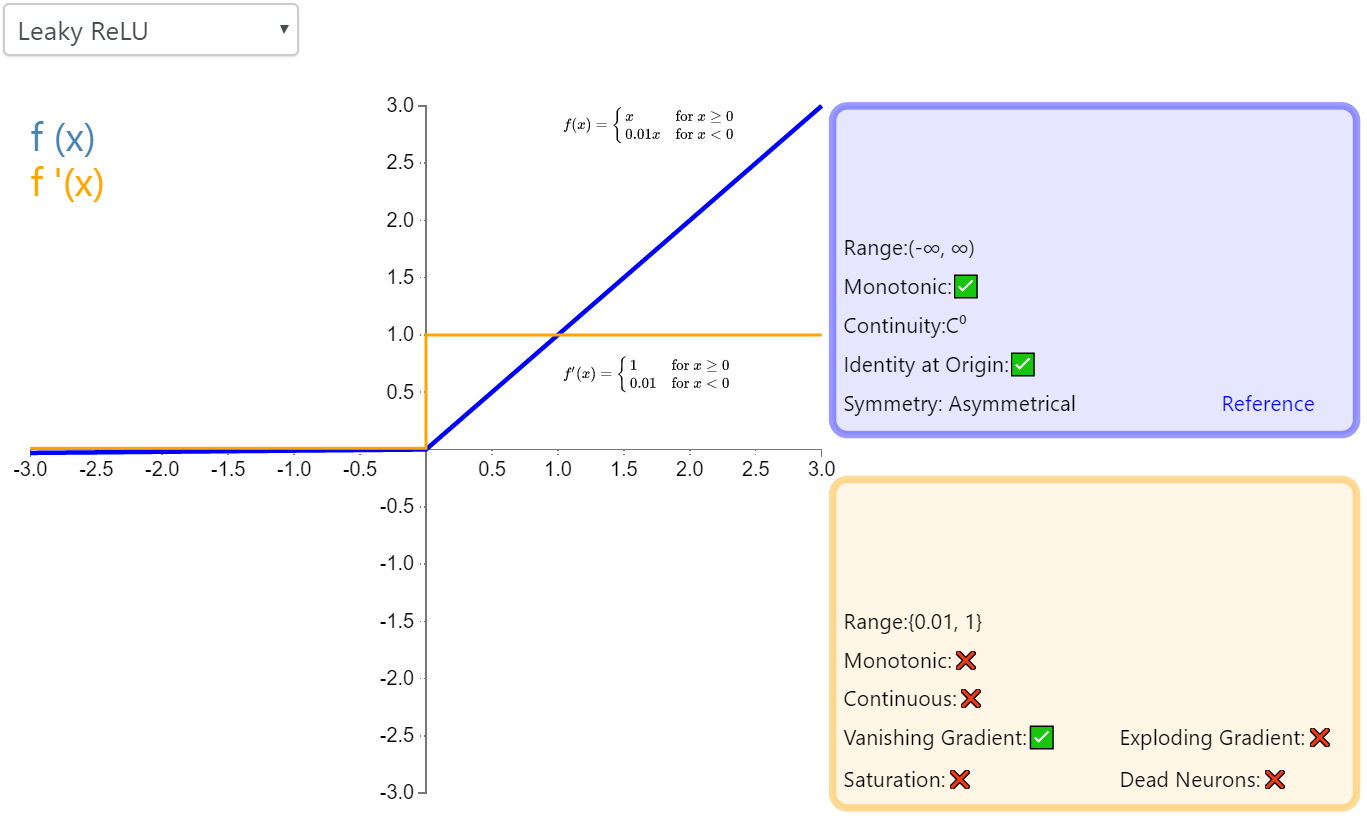
特点

• ReLU的一个变体，减少神经元死亡
• 应用较广

ELU

指数线性单元（Exponential Linear Unit，ELU）

函数形式

$$\begin{eqnarray*} f(x)&=&\left\{\begin{array}{ll} x&\text{for $x \geq 0$}\\ a(e^x-1) &\text{for $x<0$}. \end{array}\right. \\ \\ f^{\prime}(x)&=&\left\{\begin{array}{ll} 1&\text{for $x \geq 0$}\\ f(x)+a=ae^x &\text{for $x<0$}. \end{array}\right. \end{eqnarray*}$$

函数形状

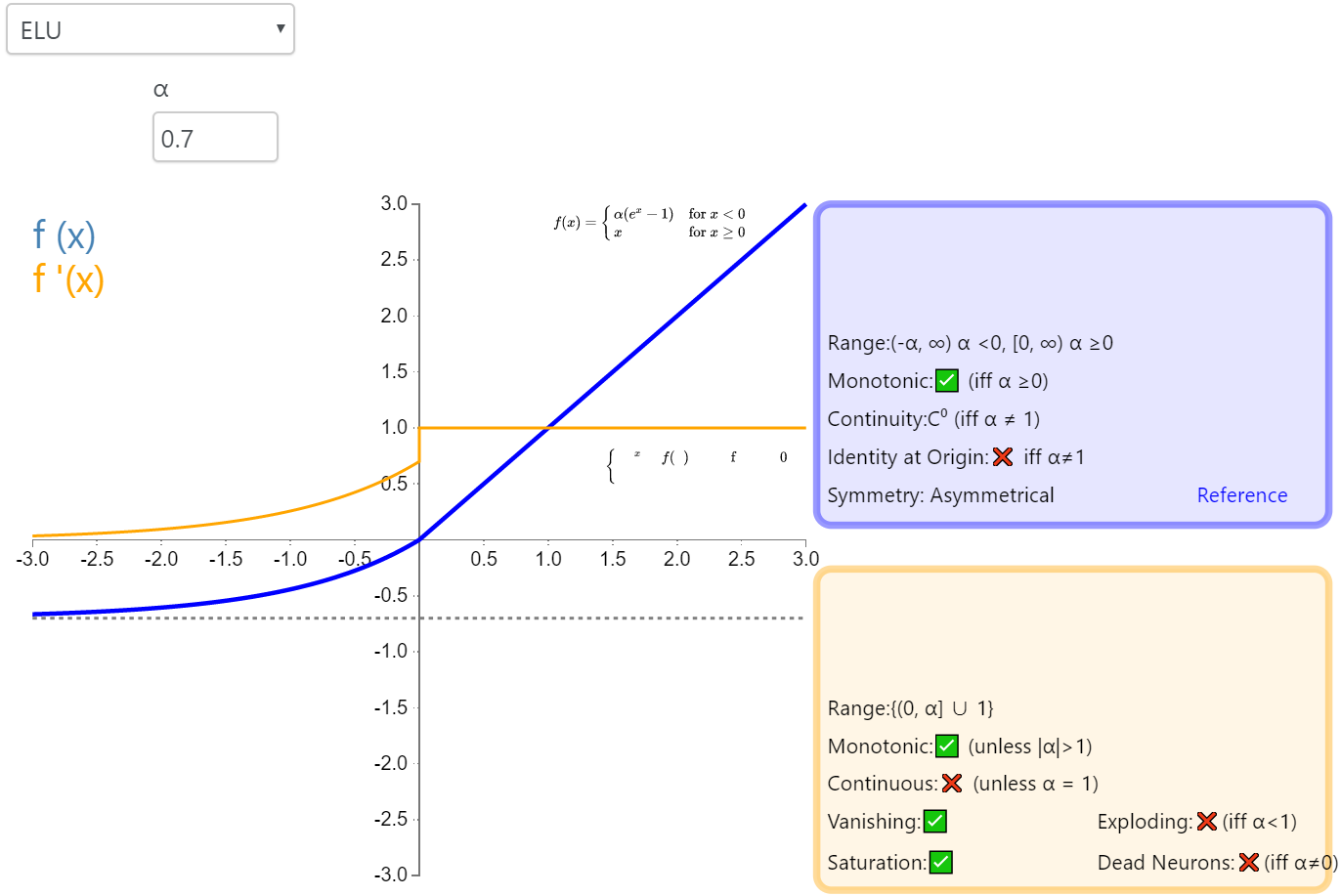
特点

• 类似于Leaky ReLU
• 计算量稍大
• 不会有Dead ReLU问题
• 均值接近于0